1.7K

《Qt 学习之路2》逐步到达尾声。尽管我们不可能在简简单单的几篇文章中将 Qt 所有内容全部涵盖（更不要说 Qt 中那些控件的使用），我想通过一定时间的学习，终究可以让文档替代这些文章。按照我的观点，这些文字仅仅是一个粗略的介绍，当你明白了大致的思路时，真正要做的，是去认真读 Qt 的文档。只有这样，才能做出自己想要的程序。当我们慢慢结束这一部分时——肯定还会有更多有关 Qt 的文章——也可以试着换下口味，来点真正的干货。

这篇文章翻译自《How does a relational database work》，在此感谢原作者辛勤的工作！

作为一个开发者，使用数据库已经成为必备技能之一。但是，我们在使用时，有没有像作者一样，希望了解数据库背后的秘密？就像我们在大学课程中学习的编译原理，实际工作中很少接触到，然而，编译技术实现的机制却会出现在很多实际应用中，不经意间，你就遇到了使用了有限自动机的框架。而这正是翻译本文的目的。或许在很长时间内，你我都不会使用到这些底层原理，但是，当有人问起类似的问题时，我们也不要故作神秘地回答说，“Magic”。

值得注意的是，文中很多概念是使用作者自己的语言给出的，并不一定是准确的定义。

是为序。

接触关系数据库时间一长，我不禁感觉到有什么东西被遗忘了。它们无处不在。我们有各种各样的数据库：从小巧有用的 SQLite 到强大的 Teradata。但是，只有少数几篇文章解释数据库是如何工作的。你可以自己搜索下“关系数据库是如何工作的”，就会发现，这个问题的答案是多么的少。并且，那些文章还都很短。现在，如果你再试着看看最时髦的技术（大数据，NoSQL 或者 JavaScript），你会发现一大堆有深度的文章，来解释它们是如何工作的。

难道是关系数据库太老了，以至于除了在大学课程、研究论文和书籍之外，都不屑于解释下它们是如何工作的？

作为一名开发者，我讨厌使用那些我不知道原理的技术。并且，数据库已经使用了 40 年了，一定有什么原因才对。多年来，我花费了几百个小时，去真正理解那些我每天都在使用的奇怪的黑箱。关系数据库很有趣，因为它们建立在有用且可重用的概念之上。如果你想了解数据库，但是却没有时间或者没有精力去研究这个广泛的主题，那么，你应该会喜欢这篇文章的。

这篇文章的题目已经明确说明，文章的目的并不是理解如何使用数据库。因此，你应该已经知道如何写出简单的连接查询语句以及基本的 CRUD 语句；否则，你可能看不懂这篇文章。这是你开始读这篇文章之前唯一需要知道的事情。其余的事，将由我来解释。

我会从一些计算机科学的概念，比如时间复杂性，开始讲起。我知道你们当中有些人讨厌这些概念，但是，没有它们，你就不能理解数据库中的那些聪明之处。由于这是一个很大的主题，我就从我认为重要的部分讲起：数据库是如何处理 SQL 语句的。我只介绍数据库背后的基本概念，这样，在文章结束的时候，你就可以对数据库中究竟发生了什么有一个比较好的概念。

这篇文章包含了大量算法和数据结构的很长的技术文章，它会需要你拿出很长时间来阅读。有些概念并不好懂，你可以暂时跳过，还是能够获得其它知识。

对于你们中的已经有一定基础的读者，这篇文章可以大致分成三个部分：

• 底层和高层的数据库组件
• 查询优化过程
• 事务和缓冲池管理

回归基础

很久很久以前（在遥远的银河系……），开发者必须知道他们代码的操作的准确数量。通过聆听算法和数据结构可以知道这个数目，因为他们不能浪费那慢得离谱的计算机的 CPU 和内存。

在本节，我会提醒你一些概念。这些概念对于理解数据库非常重要。我还会引入一个术语：数据库索引（database index）。

O(1) vs O(n²)

现在，很多开发者根本不关心时间复杂度。在一定程度上说，他们是正确的。

但是，当你处理大量数据（我说的不止几千）或者你必须要提高几毫秒时，就不得不理解这个概念了。猜猜怎么着？这两个情形都是数据库必须考虑的！我不会骚扰你很长时间，只要给我点时间来解释这个概念。这将有助于我们将来理解基于成本的优化（cost based optimization）这个概念。

概念

时间复杂度用来度量一个算法处理给定数量的数据的执行时间。为了描述时间复杂度，计算机科学家设计了大 O 标记。大 O 标记使用一个函数描述一个算法对于给定数量的输入数据需要多少操作（译注：这里所说的“操作”是一个抽象概念，可以理解为度量复杂度的一个单位）。

例如，当我说“这个算法是 O( some_function() )”时，我的意思是，对于确定数量的数据，这个算法需要 some_function(给定数量的数据) 操作来完成其工作。

重要的不是数据的数量，而是当数据的数量增加时，操作的数量是如何增加的。时间复杂度并没有给出操作的具体数量，但不失为一个好的办法。

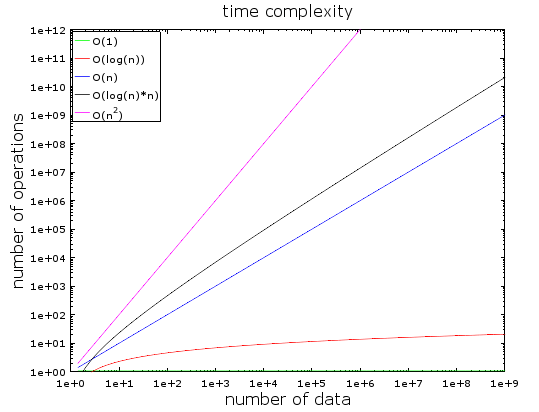
在上面图表中，你可以看到多种类型的复杂度。我使用了对数刻度去标记它们。换句话说，当数据量非常快地从一增加到十亿，我们可以发现：

• O(1) 即常数复杂度一直保持不变（否则它也不会被成为常数复杂度）。
• O(log(n)) 即使在十亿数据时也保持在比较低的位置。
• 最糟糕的是 O(n²)，其操作数非常快的暴增。
• 其它两种复杂度比较快地增加。

例子

数据量较少时，O(1) 与 O(n²) 的区别不是很明显。例如，假设你有一个算法需要处理 2000 个数据：

• O(1) 算法需要 1 个操作
• O(log(n)) 算法需要 7 个操作
• O(n) 算法需要 2000 个操作
• O(n*log(n)) 算法需要 14000 个操作
• O(n²) 算法需要 4 000 000 个操作

O(1) 和 O(n²) 的差别看起来很大（四百万）但实际上你只会损失 2 毫秒，也就是你眨巴眨巴眼镜的时间。事实上，现在的处理器每秒能够处理几千万操作。这也就是为什么在很多 IT 项目中，性能和优化往往不是什么问题。

就像我前面说的，面对海量数据时，知道这个概念还是非常重要的。现在，我们的算法需要处理 1 000 000 个数据（对于数据库而言，这也不算什么问题）：

• O(1) 算法需要 1 个操作
• O(log(n)) 算法需要 14 个操作
• O(n) 算法需要 1 000 000 个操作
• O(n*log(n)) 算法需要 14 000 000 个操作
• O(n²) 算法需要 1 000 000 000 000 个操作

我不需要真正去算算时间，不过我觉得可以这么说：使用 O(n²) 算法，你应该有时间去喝杯咖啡了（倒数第二个应该也可以的）。如果把你的数据量再加个 0，你有时间休息挺长一会儿的了。

深入一些

给你一些情形：

• 良好的哈希表的检索需要 O(1)
• 平衡树的检索需要 O(log(n))
• 数组的检索需要 O(n)
• 最好的排序算法需要 O(n*log(n))
• 不好的排序算法需要 O(n²)

注意，下一部分我们将会见到这些算法和数据结构。

时间复杂度有多种类型：

• 平均情况
• 最好情况
• 最坏情况

时间复杂度通常按照最坏情况。

我只讨论了时间复杂度，但是复杂度的概念同样适用于：

• 算法的内存消耗
• 算法的磁盘 I/O 消耗

当然，还有比 n² 更坏的复杂度，比如：

• n⁴：倒吸一口凉气！我们将要介绍的某些算法就是这个复杂度的。
• 3ⁿ：多吸一些凉气！在本文中间部分，我们会见到一个算法具有这个复杂度（这个算法在很多数据库中都有在用）。
• n 的阶乘：即便是很少的数据，你也不一定能够得到结果。
• nⁿ：如果你的算法是这个复杂度的，你应该问问自己，IT 是不是真的适合你……

注意：我并没有给你大 O 记号的准确定义，只给出了一个思想。你可以在维基百科阅读真正的定义。

合并排序

如果你要对一个集合进行排序，你要怎么做？什么？你可以调用sort()函数……好主意……但是，对于数据库，你必须知道sort()函数是怎么工作的。

有很多很好的排序算法，我们会将精力放在最重要的那个上面：合并排序。现在你可能并不明白为什么对数据进行排序很有用，但是，当你读完查询优化部分后，你就应该能够回答这个问题。另外，了解合并排序可以帮助我们弄清楚一个通用数据库合并操作：合并连接（merge join）。

合并

和很多有用的算法一样，合并排序也是基于一个小技巧：将两个已经排好序的长度为 N/2 的数组合并为一个排好序的长度为 N 的数组只需要 N 个操作。这个操作成为合并。

我们用一个简单的例子来看这是什么意思：

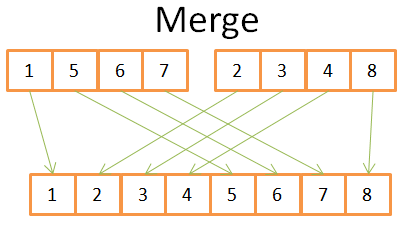
上图最终获得一个排好序的具有 8 个元素的数组，你只需要遍历两个 4 元素的数组一次。由于两个 4 元素的数组都已经排好序了：

• 1) 比较两个数组的当前元素（第一次比较时，当前元素就是第一个元素）
• 2) 取出二者之间较小的放入 8 元素数组
• 3) 取出上一步较小元素所在的那个数组的下一个元素
• 重复上述三步，直到取出其中一个数组的最后一个元素
• 将另外一个数组的剩余元素全部追加到 8 元素数组中

由于 4 元素数组已经排好序，因此上述步骤可以正常工作。你不需要在这些数组中“后退”。

现在我们已经知道了思路，下面是合并排序的伪代码：

array mergeSort(array a)
   if(length(a)==1)
      return a[0];
   end if

   // 递归调用
   [left_array right_array] := split_into_2_equally_sized_arrays(a);
   array new_left_array := mergeSort(left_array);
   array new_right_array := mergeSort(right_array);

   // 将两个已经排好序的较短的数组合并到一个较长的数组中
   array result := merge(new_left_array,new_right_array);
   return result;

合并排序将一个较大的问题分解成多个较小的问题，找到较小问题的解，从而获得原始问题的解（注意：这种类型的算法被称为“分治法”）。如果你不明白这个算法，不要担心，我第一次看到它也不明白。为了帮助理解，我将这个算法看作一个具有两个步骤的算法：

• 将数组分成较短的数组的分割阶段
• 将较短数组放在一次（使用合并）形成较长数组的排序阶段

分割阶段

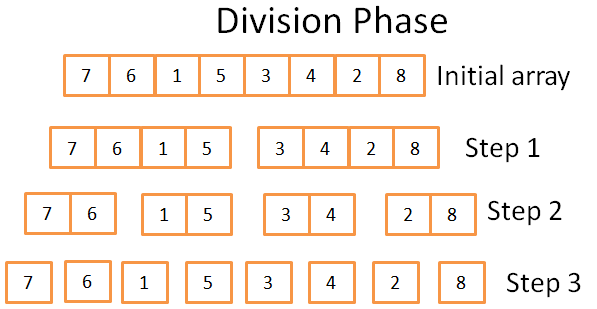
在分割阶段，使用 3 步，将原始数组分成只有一个元素的单元数组。这一步骤的计算公式是 log(N)（本例中，N=8，log(N) = 3）。

我是怎么知道这个的？

我是个天才！简而言之：数学。这一阶段的思路是，每一步将原数组的长度分成二分之一。所需要的步数就是你能够将原始数组一分为二几次。这正式对数的定义（以 2 为底）。

排序阶段

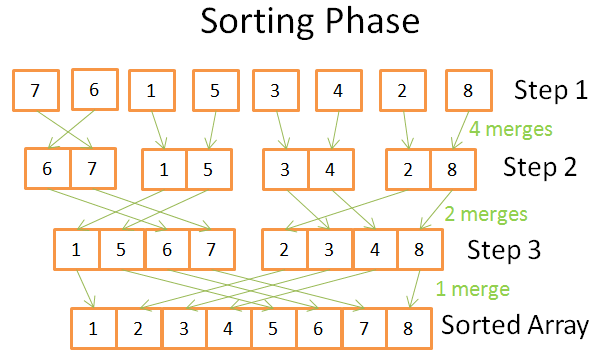
在排序阶段，你从单元数组开始。每一步都要应用多次合并，总的合并是 N=8 次：

• 第一步，你需要 4 次合并，每一次合并需要 2 个操作
• 第二步，你需要 2 次合并，每一次合并需要 4 个操作
• 第三步，你需要 1 次合并，需要 8 个操作

因为一共有 log(N) 步，所以，总的操作就是 N * log(N) 次。

合并排序的威力

为什么这个算法这么有用？

原因是：

• 你可以修改该算法，从而减少内存消耗。所需方法是，不要重新创建新的数组，而是直接修改输入的数组。注意：这种算法被称为原地算法（in-place）。
• 你可以修改该算法，使用磁盘空间和少量内存，但是又不需要大量的磁盘 I/O 消耗。其思路是，只在内存中加载当前正在处理的部分。当你需要对几个 G 的数据表进行排序，但内存缓存只有 100M 的时候，这是一种很重要的方法。注意：这种算法被称为外部排序（external sorting）。
• 你可以修改该算法，以便在多个处理器/线程/服务器中运行。例如，分布式合并排序是 Hadoop 的核心组件之一（Hadoop 是处理大数据的重要框架之一）。
• 这个算法可以变成真金白银（真事儿！）。

这种排序算法被绝大多数（即便不能说全部）数据库采用，但它也并不是唯一的排序算法。如果你想知道得更多，你可以阅读这篇研究论文。该论文讨论了数据库中使用的各种通用排序算法的优缺点。